The International System of Units (SI, abbreviated from the French Système international (d'unités)) is the modern form of the metric system and is the most widely used system of measurement[citation needed]. It comprises a coherent system of units of measurement built on seven base units, which are the second, metre, kilogram, ampere, kelvin, mole, candela, and a set of twenty prefixes to the unit names and unit symbols that may be used when specifying multiples and fractions of the units. The system also specifies names for 22 derived units, such as lumen and watt, for other common physical quantities.
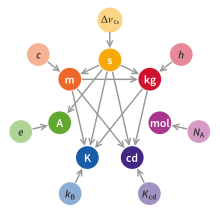
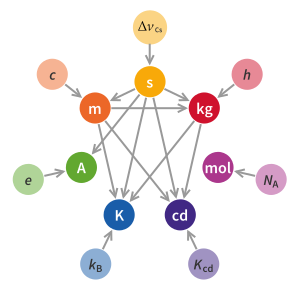
The base units are defined in terms of invariant constants of nature, such as the speed of light in vacuum and the charge of the electron, which can be observed and measured with great accuracy. Seven constants are used in various combinations to define the seven base units. Prior to 2019, artefacts were used instead of some of these constants, the last being the International Prototype of the Kilogram, a cylinder of platinum-iridium. Concern regarding its stability led to a revision of the definition of the base units entirely in terms of constants of nature, which was put into effect on 20 May 2019.[1]
Derived units may be defined in terms of base units or other derived units. They are adopted to facilitate measurement of diverse quantities. The SI is intended to be an evolving system; units and prefixes are created and unit definitions are modified through international agreement as the technology of measurement progresses and the precision of measurements improves. The most recently named derived unit, the katal, was defined in 1999.
The reliability of the SI depends not only on the precise measurement of standards for the base units in terms of various physical constants of nature, but also on precise definition of those constants. The set of underlying constants is modified as more stable constants are found, or may be more precisely measured. For example, in 1983 the metre was redefined as the distance that light propagates in vacuum in a given fraction of a second, thus making the value of the speed of light in terms of the defined units exact.
The motivation for the development of the SI was the diversity of units that had sprung up within the centimetre–gram–second (CGS) systems (specifically the inconsistency between the systems of electrostatic units and electromagnetic units) and the lack of coordination between the various disciplines that used them. The General Conference on Weights and Measures (French: Conférence générale des poids et mesures – CGPM), which was established by the Metre Convention of 1875, brought together many international organisations to establish the definitions and standards of a new system and to standardise the rules for writing and presenting measurements. The system was published in 1960 as a result of an initiative that began in 1948. It is based on the metre–kilogram–second system of units (MKS) rather than any variant of the CGS.
nits and prefixes[edit]
The International System of Units consists of a set of base units, derived units, and a set of decimal-based multipliers that are used as prefixes.[2]:103–106 The units, excluding prefixed units,[Note 1] form a coherent system of units, which is based on a system of quantities in such a way that the equations between the numerical values expressed in coherent units have exactly the same form, including numerical factors, as the corresponding equations between the quantities. For example, 1 N = 1 kg × 1 m/s2 says that one newton is the force required to accelerate a mass of one kilogram at one metre per second squared, as related through the principle of coherence to the equation relating the corresponding quantities: F = m × a.
Derived units apply to derived quantities, which may by definition be expressed in terms of base quantities, and thus are not independent; for example, electrical conductance is the inverse of electrical resistance, with the consequence that the siemens is the inverse of the ohm, and similarly, the ohm and siemens can be replaced with a ratio of an ampere and a volt, because those quantities bear a defined relationship to each other.[Note 2] Other useful derived quantities can be specified in terms of the SI base and derived units that have no named units in the SI system, such as acceleration, which is defined in SI units as m/s2.
Base units[edit]
The SI base units are the building blocks of the system and all the other units are derived from them.
| Unit name | Unit symbol | Dimension symbol | Quantity name | Definition |
|---|---|---|---|---|
| second [n 1] | s | T | time | The duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom. |
| metre | m | L | length | The distance travelled by light in vacuum in 1299792458 second. |
| kilogram [n 2] | kg | M | mass | The kilogram is defined by setting the Planck constant h exactly to 6.62607015×10−34 J⋅s (J = kg⋅m2⋅s−2), given the definitions of the metre and the second.[1] |
| ampere | A | I | electric current | The flow of 11.602176634×10−19 times the elementary charge e per second. |
| kelvin | K | Θ | thermodynamic temperature | The kelvin is defined by setting the fixed numerical value of the Boltzmann constant k to 1.380649×10−23 J⋅K−1, (J = kg⋅m2⋅s−2), given the definition of the kilogram, the metre, and the second. |
| mole | mol | N | amount of substance | The amount of substance of exactly 6.02214076×1023 elementary entities.[n 3] This number is the fixed numerical value of the Avogadro constant, NA, when expressed in the unit mol−1 and is called the Avogadro number. |
| candela | cd | J | luminous intensity | The luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 5.4×1014 hertz and that has a radiant intensity in that direction of 1683 watt per steradian. |
| ||||
Derived units[edit]
The derived units in the SI are formed by powers, products, or quotients of the base units and are potentially unlimited in number.[2]:103[3]:14,16 Derived units are associated with derived quantities; for example, velocity is a quantity that is derived from the base quantities of time and length, and thus the SI derived unit is metre per second (symbol m/s). The dimensions of derived units can be expressed in terms of the dimensions of the base units.
Combinations of base and derived units may be used to express other derived units. For example, the SI unit of force is the newton (N), the SI unit of pressure is the pascal (Pa)—and the pascal can be defined as one newton per square metre (N/m2).[6]
| Name | Symbol | Quantity | In SI base units | In other SI units |
|---|---|---|---|---|
| radiannote 1 | rad | plane angle | m/m | 1 |
| steradiannote 1 | sr | solid angle | m2/m2 | 1 |
| hertz | Hz | frequency | s−1 | |
| newton | N | force, weight | kg⋅m⋅s−2 | |
| pascal | Pa | pressure, stress | kg⋅m−1⋅s−2 | N/m2 |
| joule | J | energy, work, heat | kg⋅m2⋅s−2 | N⋅m = Pa⋅m3 |
| watt | W | power, radiant flux | kg⋅m2⋅s−3 | J/s |
| coulomb | C | electric charge or quantity of electricity | s⋅A | |
| volt | V | voltage (electrical potential), emf | kg⋅m2⋅s−3⋅A−1 | W/A = J/C |
| farad | F | capacitance | kg−1⋅m−2⋅s4⋅A2 | C/V |
| ohm | Ω | resistance, impedance, reactance | kg⋅m2⋅s−3⋅A−2 | V/A |
| siemens | S | electrical conductance | kg−1⋅m−2⋅s3⋅A2 | Ω−1 |
| weber | Wb | magnetic flux | kg⋅m2⋅s−2⋅A−1 | V⋅s |
| tesla | T | magnetic flux density | kg⋅s−2⋅A−1 | Wb/m2 |
| henry | H | inductance | kg⋅m2⋅s−2⋅A−2 | Wb/A |
| degree Celsius | °C | temperature relative to 273.15 K | K | |
| lumen | lm | luminous flux | cd⋅sr | cd⋅sr |
| lux | lx | illuminance | m−2⋅cd | lm/m2 |
| becquerel | Bq | radioactivity (decays per unit time) | s−1 | |
| gray | Gy | absorbed dose (of ionising radiation) | m2⋅s−2 | J/kg |
| sievert | Sv | equivalent dose (of ionising radiation) | m2⋅s−2 | J/kg |
| katal | kat | catalytic activity | mol⋅s−1 | |
| Notes 1. The radian and steradian are defined as dimensionless derived units. | ||||
| Name | Symbol | Derived quantity | Typical symbol |
|---|---|---|---|
| square metre | m2 | area | A |
| cubic metre | m3 | volume | V |
| metre per second | m/s | speed, velocity | v |
| metre per second squared | m/s2 | acceleration | a |
| reciprocal metre | m−1 | wavenumber | σ, ṽ |
| vergence (optics) | V, 1/f | ||
| kilogram per cubic metre | kg/m3 | density | ρ |
| kilogram per square metre | kg/m2 | surface density | ρA |
| cubic metre per kilogram | m3/kg | specific volume | v |
| ampere per square metre | A/m2 | current density | j |
| ampere per metre | A/m | magnetic field strength | H |
| mole per cubic metre | mol/m3 | concentration | c |
| kilogram per cubic metre | kg/m3 | mass concentration | ρ, γ |
| candela per square metre | cd/m2 | luminance | Lv |
| Name | Symbol | Quantity | In SI base units |
|---|---|---|---|
| pascal second | Pa⋅s | dynamic viscosity | m−1⋅kg⋅s−1 |
| newton metre | N⋅m | moment of force | m2⋅kg⋅s−2 |
| newton per metre | N/m | surface tension | kg⋅s−2 |
| radian per second | rad/s | angular velocity | s−1 |
| radian per second squared | rad/s2 | angular acceleration | s−2 |
| watt per square metre | W/m2 | heat flux density | kg⋅s−3 |
| joule per kelvin | J/K | heat capacity, entropy | m2⋅kg⋅s−2⋅K−1 |
| joule per kilogram kelvin | J/(kg⋅K) | specific heat capacity, specific entropy | m2⋅s−2⋅K−1 |
| joule per kilogram | J/kg | specific energy | m2⋅s−2 |
| watt per metre kelvin | W/(m⋅K) | thermal conductivity | m⋅kg⋅s−3⋅K−1 |
| joule per cubic metre | J/m3 | energy density | m−1⋅kg⋅s−2 |
| volt per metre | V/m | electric field strength | m⋅kg⋅s−3⋅A−1 |
| coulomb per cubic metre | C/m3 | electric charge density | m−3⋅s⋅A |
| coulomb per square metre | C/m2 | surface charge density, electric flux density | m−2⋅s⋅A |
| farad per metre | F/m | permittivity | m−3⋅kg−1⋅s4⋅A2 |
| henry per metre | H/m | permeability | m⋅kg⋅s−2⋅A−2 |
| joule per mole | J/mol | molar energy | m2⋅kg⋅s−2⋅mol−1 |
| joule per mole kelvin | J/(mol⋅K) | molar heat capacity, molar entropy | m2⋅kg⋅s−2⋅K−1⋅mol−1 |
| coulomb per kilogram | C/kg | exposure | kg−1⋅s⋅A |
| gray per second | Gy/s | absorbed dose rate | m2⋅s−3 |
| watt per steradian | W/sr | radiant intensity | m2⋅kg⋅s−3 |
| watt per square metre steradian | W/(m2⋅sr) | radiance | kg⋅s−3 |
| katal per cubic metre | kat/m3 | catalytic activity concentration | m−3⋅s−1⋅mol |
Prefixes[edit]
Prefixes are added to unit names to produce multiples and submultiples of the original unit. All of these are integer powers of ten, and above a hundred or below a hundredth all are integer powers of a thousand. For example, kilo- denotes a multiple of a thousand and milli- denotes a multiple of a thousandth, so there are one thousand millimetres to the metre and one thousand metres to the kilometre. The prefixes are never combined, so for example a millionth of a metre is a micrometre, not a millimillimetre. Multiples of the kilogram are named as if the gram were the base unit, so a millionth of a kilogram is a milligram, not a microkilogram.[2]:122[7]:14 When prefixes are used to form multiples and submultiples of SI base and derived units, the resulting units are no longer coherent.[2]:7
The BIPM specifies 20 prefixes for the International System of Units (SI):
| Prefix | Base 10 | Base 1000 | Decimal | English word | Adoption[nb 1] | ||
|---|---|---|---|---|---|---|---|
| Name | Symbol | Short scale | Long scale | ||||
| yotta | Y | 1024 | 10008 | 1000000000000000000000000 | septillion | quadrillion | 1991 |
| zetta | Z | 1021 | 10007 | 1000000000000000000000 | sextillion | trilliard | 1991 |
| exa | E | 1018 | 10006 | 1000000000000000000 | quintillion | trillion | 1975 |
| peta | P | 1015 | 10005 | 1000000000000000 | quadrillion | billiard | 1975 |
| tera | T | 1012 | 10004 | 1000000000000 | trillion | billion | 1960 |
| giga | G | 109 | 10003 | 1000000000 | billion | milliard | 1960 |
| mega | M | 106 | 10002 | 1000000 | million | 1873 | |
| kilo | k | 103 | 10001 | 1000 | thousand | 1795 | |
| hecto | h | 102 | 10002/3 | 100 | hundred | 1795 | |
| deca | da | 101 | 10001/3 | 10 | ten | 1795 | |
| 100 | 10000 | 1 | one | – | |||
| deci | d | 10−1 | 1000−1/3 | 0.1 | tenth | 1795 | |
| centi | c | 10−2 | 1000−2/3 | 0.01 | hundredth | 1795 | |
| milli | m | 10−3 | 1000−1 | 0.001 | thousandth | 1795 | |
| micro | μ | 10−6 | 1000−2 | 0.000001 | millionth | 1873 | |
| nano | n | 10−9 | 1000−3 | 0.000000001 | billionth | milliardth | 1960 |
| pico | p | 10−12 | 1000−4 | 0.000000000001 | trillionth | billionth | 1960 |
| femto | f | 10−15 | 1000−5 | 0.000000000000001 | quadrillionth | billiardth | 1964 |
| atto | a | 10−18 | 1000−6 | 0.000000000000000001 | quintillionth | trillionth | 1964 |
| zepto | z | 10−21 | 1000−7 | 0.000000000000000000001 | sextillionth | trilliardth | 1991 |
| yocto | y | 10−24 | 1000−8 | 0.000000000000000000000001 | septillionth | quadrillionth | 1991 |
| |||||||
Non-SI units accepted for use with SI[edit]
Many non-SI units continue to be used in the scientific, technical, and commercial literature. Some units are deeply embedded in history and culture, and their use has not been entirely replaced by their SI alternatives. The CIPM recognised and acknowledged such traditions by compiling a list of non-SI units accepted for use with SI:[2]
Some units of time, angle, and legacy non-SI units have a long history of use. Most societies have used the solar day and its non-decimal subdivisions as a basis of time and, unlike the foot or the pound, these were the same regardless of where they were being measured. The radian, being 12π of a revolution, has mathematical advantages but is rarely used for navigation. Further, the units used in navigation around the world are similar. The tonne, litre, and hectare were adopted by the CGPM in 1879 and have been retained as units that may be used alongside SI units, having been given unique symbols. The catalogued units are given below:
| Quantity | Name | Symbol | Value in SI units |
|---|---|---|---|
| time | minute | min | 1 min = 60 s |
| hour | h | 1 h = 60 min = 3600 s | |
| day | d | 1 d = 24 h = 86400 s | |
| length | astronomical unit | au | 1 au = 149597870700 m |
| plane and phase angle | degree | ° | 1° = (π/180) rad |
| minute | ′ | 1′ = (1/60)° = (π/10800) rad | |
| second | ″ | 1″ = (1/60)′ = (π/648000) rad | |
| area | hectare | ha | 1 ha = 1 hm2 = 104 m2 |
| volume | litre | l, L | 1 l = 1 L = 1 dm3 = 103 cm3 = 10−3 m3 |
| mass | tonne (metric ton) | t | 1 t = 1000 kg |
| dalton | Da | 1 Da = 1.660539040(20)×10−27 kg | |
| energy | electronvolt | eV | 1 eV = 1.602176634×10−19 J |
| logarithmic ratio quantities | neper | Np | In using these units it is important that the nature of the quantity be specified and that any reference value used be specified. |
| bel | B | ||
| decibel | dB |
These units are used in combination with SI units in common units such as the kilowatt-hour (1 kW⋅h = 3.6 MJ).
Common notions of the metric units[edit]
The basic units of the metric system, as originally defined, represented common quantities or relationships in nature. They still do – the modern precisely defined quantities are refinements of definition and methodology, but still with the same magnitudes. In cases where laboratory precision may not be required or available, or where approximations are good enough, the original definitions may suffice.[Note 3]
- A second is 1/60 of a minute, which is 1/60 of an hour, which is 1/24 of a day, so a second is 1/86400 of a day (the use of base 60 dates back to Babylonian times); a second is the time it takes a dense object to freely fall 4.9 metres from rest.
- The length of the equator is close to 40000000 m (more precisely 40075014.2 m).[8] In fact, the dimensions of our planet were used by the French Academy in the original definition of the metre.[9]
- The metre is close to the length of a pendulum that has a period of 2 seconds;[Note 4] most dining tabletops are about 0.75 metres high;[10] a very tall human (basketball forward) is about 2 metres tall.[11]
- The kilogram is the mass of a litre of cold water; a cubic centimetre or millilitre of water has a mass of one gram; a 1-euro coin weighs 7.5 g;[12] a Sacagawea US 1-dollar coinweighs 8.1 g;[13] a UK 50-pence coin weighs 8.0 g.[14]
- A candela is about the luminous intensity of a moderately bright candle, or 1 candle power; a 60 W tungsten-filament incandescent light bulb has a luminous intensity of about 64 candela.
- A mole of a substance has a mass that is its molecular mass expressed in units of grams; the mass of a mole of carbon is 12.0 g, and the mass of a mole of table salt is 58.4 g.
- Since all gases have the same volume per mole at a given temperature and pressure far from their points of liquefaction and solidification (see Perfect gas), and air is about 1/5 oxygen (molecular mass 32) and 4/5 nitrogen (molecular mass 28), the density of any near-perfect gas relative to air can be obtained to a good approximation by dividing its molecular mass by 29 (because 4/5 × 28 + 1/5 × 32 = 28.8 ≈ 29). For example carbon monoxide (molecular mass 28) has almost the same density as air.
- A temperature difference of one kelvin is the same as one degree Celsius: 1/100 of the temperature differential between the freezing and boiling points of water at sea level; the absolute temperature in kelvins is the temperature in degrees Celsius plus about 273; human body temperature is about 37 °C or 310 K.
- A 60 W incandescent light bulb rated at 120 V (US mains voltage) consumes 0.5 A at this voltage. A 60 W bulb rated at 240 V (European mains voltage) consumes 0.25 A at this voltage.
Lexicographic conventions[edit]
Unit names[edit]
The symbols for the SI units are intended to be identical, regardless of the language used,[2]:130–135 but unit names are ordinary nouns and use the character set and follow the grammatical rules of the language concerned. Names of units follow the grammatical rules associated with common nouns: in English and in French they start with a lowercase letter (e.g., newton, hertz, pascal), even when the symbol for the unit begins with a capital letter. This also applies to "degrees Celsius", since "degree" is the unit.[15][16] The English spelling for certain SI units differs: US English uses the spelling deka-, meter, and liter, whilst International English more commonly uses deca-, metre, and litre.
Unit symbols and the values of quantities [edit]
Although the writing of unit names is language-specific, the writing of unit symbols and the values of quantities is consistent across all languages and therefore the SI Brochure has specific rules in respect of writing them.[2]:130–135 The guideline produced by the National Institute of Standards and Technology (NIST)[17] clarifies language-specific areas in respect of American English that were left open by the SI Brochure, but is otherwise identical to the SI Brochure.[18]
General rules[edit]
General rules[Note 5] for writing SI units and quantities apply to text that is either handwritten or produced using an automated process:
- The value of a quantity is written as a number followed by a space (representing a multiplication sign) and a unit symbol; e.g., 2.21 kg, 7.3×102 m2, 22 K. This rule explicitly includes the percent sign (%)[2]:134 and the symbol for degrees Celsius (°C).[2]:133 Exceptions are the symbols for plane angular degrees, minutes, and seconds (°, ′, and ″), which are placed immediately after the number with no intervening space.
- Symbols are mathematical entities, not abbreviations, and as such do not have an appended period/full stop (.), unless the rules of grammar demand one for another reason, such as denoting the end of a sentence.
- A prefix is part of the unit, and its symbol is prepended to a unit symbol without a separator (e.g., k in km, M in MPa, G in GHz, μ in μg). Compound prefixes are not allowed. A prefixed unit is atomic in expressions (e.g., km2 is equivalent to (km)2).
- Unit symbols are written using roman (upright) type, regardless of the type used in the surrounding text.
- Symbols for derived units formed by multiplication are joined with a centre dot (⋅) or a non-breaking space; e.g., N⋅m or N m.
- Symbols for derived units formed by division are joined with a solidus (/), or given as a negative exponent. E.g., the "metre per second" can be written m/s, m s−1, m⋅s−1, or ms. A solidus must not be used more than once in a given expression without parentheses to remove ambiguities; e.g., kg/(m⋅s2) and kg⋅m−1⋅s−2 are acceptable, but kg/m/s2 is ambiguous and unacceptable.
- The first letter of symbols for units derived from the name of a person is written in upper case; otherwise, they are written in lower case. E.g., the unit of pressure is named after Blaise Pascal, so its symbol is written "Pa", but the symbol for mole is written "mol". Thus, "T" is the symbol for tesla, a measure of magnetic field strength, and "t" the symbol for tonne, a measure of mass. Since 1979, the litre may exceptionally be written using either an uppercase "L" or a lowercase "l", a decision prompted by the similarity of the lowercase letter "l" to the numeral "1", especially with certain typefaces or English-style handwriting. The American NIST recommends that within the United States "L" be used rather than "l".
- Symbols do not have a plural form, e.g., 25 kg, but not 25 kgs.
- Uppercase and lowercase prefixes are not interchangeable. E.g., the quantities 1 mW and 1 MW represent two different quantities (milliwatt and megawatt).
- The symbol for the decimal marker is either a point or comma on the line. In practice, the decimal point is used in most English-speaking countries and most of Asia, and the comma in most of Latin America and in continental European countries.[19]
- Spaces should be used as a thousands separator (1000000) in contrast to commas or periods (1,000,000 or 1.000.000) to reduce confusion resulting from the variation between these forms in different countries.
- Any line-break inside a number, inside a compound unit, or between number and unit should be avoided. Where this is not possible, line breaks should coincide with thousands separators.
- Because the value of "billion" and "trillion" varies between languages, the dimensionless terms "ppb" (parts per billion) and "ppt" (parts per trillion) should be avoided. The SI Brochure does not suggest alternatives.
Printing SI symbols[edit]
The rules covering printing of quantities and units are part of ISO 80000-1:2009.[20]
Further rules[Note 5] are specified in respect of production of text using printing presses, word processors, typewriters, and the like.
International System of Quantities[edit]
-
-
-
-
- SI Brochure
-
-
-
The CGPM publishes a brochure that defines and presents the SI.[2] Its official version is in French, in line with the Metre Convention.[2]:102 It leaves some scope for local interpretation, particularly regarding names and terms in different languages.[Note 6][3]
The writing and maintenance of the CGPM brochure is carried out by one of the committees of the International Committee for Weights and Measures (CIPM). The definitions of the terms "quantity", "unit", "dimension" etc. that are used in the SI Brochure are those given in the International vocabulary of metrology.[21]
The quantities and equations that provide the context in which the SI units are defined are now referred to as the International System of Quantities (ISQ). The system is based on the quantities underlying each of the seven base units of the SI. Other quantities, such as area, pressure, and electrical resistance, are derived from these base quantities by clear non-contradictory equations. The ISQ defines the quantities that are measured with the SI units.[22] The ISQ is defined in the international standard ISO/IEC 80000, and was finalised in 2009 with the publication of ISO 80000-1.[23]
Realisation of units[edit]
Metrologists carefully distinguish between the definition of a unit and its realisation. The definition of each base unit of the SI is drawn up so that it is unique and provides a sound theoretical basis on which the most accurate and reproducible measurements can be made. The realisation of the definition of a unit is the procedure by which the definition may be used to establish the value and associated uncertainty of a quantity of the same kind as the unit. A description of the mise en pratique[Note 7] of the base units is given in an electronic appendix to the SI Brochure.[25][2]:168–169
The published mise en pratique is not the only way in which a base unit can be determined: the SI Brochure states that "any method consistent with the laws of physics could be used to realise any SI unit."[2]:111 In the current (2016) exercise to overhaul the definitions of the base units, various consultative committees of the CIPM have required that more than one mise en pratique shall be developed for determining the value of each unit.[citation needed] In particular:
- At least three separate experiments be carried out yielding values having a relative standard uncertainty in the determination of the kilogram of no more than 5×10−8 and at least one of these values should be better than 2×10−8. Both the Kibble balance and the Avogadro project should be included in the experiments and any differences between these be reconciled.[26][27]
- When the kelvin is being determined, the relative uncertainty of the Boltzmann constant derived from two fundamentally different methods such as acoustic gas thermometry and dielectric constant gas thermometry be better than one part in 10−6 and that these values be corroborated by other measurements.[28]
Evolution of the SI[edit]
Changes to the SI[edit]
The International Bureau of Weights and Measures (BIPM) has described SI as "the modern metric system".[2]:95 Changing technology has led to an evolution of the definitions and standards that has followed two principal strands – changes to SI itself, and clarification of how to use units of measure that are not part of SI but are still nevertheless used on a worldwide basis.
Since 1960 the CGPM has made a number of changes to the SI to meet the needs of specific fields, notably chemistry and radiometry. These are mostly additions to the list of named derived units, and include the mole (symbol mol) for an amount of substance, the pascal (symbol Pa) for pressure, the siemens (symbol S) for electrical conductance, the becquerel (symbol Bq) for "activity referred to a radionuclide", the gray (symbol Gy) for ionising radiation, the sievert (symbol Sv) as the unit of dose equivalent radiation, and the katal (symbol kat) for catalytic activity.[2]:156[29][2]:156[2]:158[2]:159[2]:165
Acknowledging the advancement of precision science at both large and small scales, the range of defined prefixes pico- (10−12) to tera- (1012) was extended to 10−24 to 1024.[2]:152[2]:158[2]:164
The 1960 definition of the standard metre in terms of wavelengths of a specific emission of the krypton 86 atom was replaced with the distance that light travels in a vacuum in exactly 1299792458 second, so that the speed of light is now an exactly specified constant of nature.
A few changes to notation conventions have also been made to alleviate lexicographic ambiguities. An analysis under the aegis of CSIRO, published in 2009 by the Royal Society, has pointed out the opportunities to finish the realisation of that goal, to the point of universal zero-ambiguity machine readability.[30]
2019 redefinitions[edit]
After the metre was redefined in 1960, the kilogram remained the only SI base unit directly based on a specific physical artefact, the International Prototype of the Kilogram (IPK), for its definition and thus the only unit that was still subject to periodic comparisons of national standard kilograms with the IPK.[31] During the 2nd and 3rd Periodic Verification of National Prototypes of the Kilogram, a significant divergence had occurred between the mass of the IPK and all of its official copies stored around the world: the copies had all noticeably increased in mass with respect to the IPK. During extraordinary verifications carried out in 2014 preparatory to redefinition of metric standards, continuing divergence was not confirmed. Nonetheless, the residual and irreducible instability of a physical IPK undermined the reliability of the entire metric system to precision measurement from small (atomic) to large (astrophysical) scales.
A proposal was made that:
- In addition to the speed of light, four constants of nature – the Planck constant, an elementary charge, the Boltzmann constant, and the Avogadro number – be defined to have exact values
- The International Prototype Kilogram be retired
- The current definitions of the kilogram, ampere, kelvin, and mole be revised
- The wording of base unit definitions should change emphasis from explicit unit to explicit constant definitions.
In 2015, the CODATA task group on fundamental constants announced special submission deadlines for data to compute the final values for the new definitions.[32]
The new definitions were adopted at the 26th CGPM on 16 November 2018, and came into effect on 20 May 2019.[33] The change was adopted by the European Union through Directive (EU) 2019/1258.[34]
History[edit]
The improvisation of units[edit]
The units and unit magnitudes of the metric system which became the SI were improvised piecemeal from everyday physical quantities starting in the mid-18th century. Only later were they moulded into an orthogonal coherent decimal system of measurement.
The degree centigrade as a unit of temperature resulted from the scale devised by Swedish astronomer Anders Celsius in 1742. His scale counter-intuitively designated 100 as the freezing point of water and 0 as the boiling point. Independently, in 1743, the French physicist Jean-Pierre Christindescribed a scale with 0 as the freezing point of water and 100 the boiling point. The scale became known as the centi-grade, or 100 gradations of temperature, scale.
The metric system was developed from 1791 onwards by a committee of the French Academy of Sciences, commissioned to create a unified and rational system of measures.[36] The group, which included preeminent French men of science,[37]:89 used the same principles for relating length, volume, and mass that had been proposed by the English clergyman John Wilkins in 1668[38][39] and the concept of using the Earth's meridian as the basis of the definition of length, originally proposed in 1670 by the French abbot Mouton.[40][41]
In March 1791, the Assembly adopted the committee's proposed principles for the new decimal system of measure including the metre defined to be 1/10,000,000 of the length of the quadrant of earth's meridian passing through Paris, and authorised a survey to precisely establish the length of the meridian. In July 1792, the committee proposed the names metre, are, litre and grave for the units of length, area, capacity, and mass, respectively. The committee also proposed that multiples and submultiples of these units were to be denoted by decimal-based prefixes such as centi for a hundredth and kilo for a thousand.[42]:82
Later, during the process of adoption of the metric system, the Latin gramme and kilogramme, replaced the former provincial terms gravet (1/1000 grave) and grave. In June 1799, based on the results of the meridian survey, the standard mètre des Archives and kilogramme des Archives were deposited in the French National Archives. Subsequently, that year, the metric system was adopted by law in France.[48] [49] The French system was short-lived due to its unpopularity. Napoleon ridiculed it, and in 1812, introduced a replacement system, the mesures usuelles or "customary measures" which restored many of the old units, but redefined in terms of the metric system.
During the first half of the 19th century there was little consistency in the choice of preferred multiples of the base units: typically the myriametre (10000 metres) was in widespread use in both France and parts of Germany, while the kilogram (1000 grams) rather than the myriagram was used for mass.[35]
In 1832, the German mathematician Carl Friedrich Gauss, assisted by Wilhelm Weber, implicitly defined the second as a base unit when he quoted the Earth's magnetic field in terms of millimetres, grams, and seconds.[43] Prior to this, the strength of the Earth's magnetic field had only been described in relative terms. The technique used by Gauss was to equate the torqueinduced on a suspended magnet of known mass by the Earth's magnetic field with the torque induced on an equivalent system under gravity. The resultant calculations enabled him to assign dimensions based on mass, length and time to the magnetic field.[Note 8][50]
A candlepower as a unit of illuminance was originally defined by an 1860 English law as the light produced by a pure spermaceti candle weighing 1⁄6 pound (76 grams) and burning at a specified rate. Spermaceti, a waxy substance found in the heads of sperm whales, was once used to make high-quality candles. At this time the French standard of light was based upon the illumination from a Carcel oil lamp. The unit was defined as that illumination emanating from a lamp burning pure rapeseed oil at a defined rate. It was accepted that ten standard candles were about equal to one Carcel lamp.
Metre Convention[edit]
A French-inspired initiative for international cooperation in metrology led to the signing in 1875 of the Metre Convention, also called Treaty of the Metre, by 17 nations.[Note 9][37]:353–354 Initially the convention only covered standards for the metre and the kilogram. In 1921, the Metre Convention was extended to include all physical units, including the ampere and others thereby enabling the CGPM to address inconsistencies in the way that the metric system had been used.[44][2]:96
A set of 30 prototypes of the metre and 40 prototypes of the kilogram,[Note 10] in each case made of a 90% platinum-10% iridium alloy, were manufactured by British metallurgy specialty firm and accepted by the CGPM in 1889. One of each was selected at random to become the International prototype metre and International prototype kilogram that replaced the mètre des Archives and kilogramme des Archives respectively. Each member state was entitled to one of each of the remaining prototypes to serve as the national prototype for that country.[51]
The treaty also established a number of international organisations to oversee the keeping of international standards of measurement:[52] [53]
The CGS and MKS systems[edit]
This section is missing information about all 22 named derived units of SI. (December 2017)
|
This section is missing information about a period of ~35-40 years between early 20th century and end of WW2 covering most of the industrial revolution. (December 2017)
|
In the 1860s, James Clerk Maxwell, William Thomson (later Lord Kelvin) and others working under the auspices of the British Association for the Advancement of Science, built on Gauss's work and formalised the concept of a coherent system of units with base units and derived units christened the centimetre–gram–second system of units in 1874. The principle of coherence was successfully used to define a number of units of measure based on the CGS, including the erg for energy, the dyne for force, the barye for pressure, the poise for dynamic viscosity and the stokes for kinematic viscosity.[46]
In 1879, the CIPM published recommendations for writing the symbols for length, area, volume and mass, but it was outside its domain to publish recommendations for other quantities. Beginning in about 1900, physicists who had been using the symbol "μ" (mu) for "micrometre" or "micron", "λ" (lambda) for "microlitre", and "γ" (gamma) for "microgram" started to use the symbols "μm", "μL" and "μg".[54]
At the close of the 19th century three different systems of units of measure existed for electrical measurements: a CGS-based system for electrostatic units, also known as the Gaussian or ESU system, a CGS-based system for electromechanical units (EMU) and an International system based on units defined by the Metre Convention.[55] for electrical distribution systems. Attempts to resolve the electrical units in terms of length, mass, and time using dimensional analysis was beset with difficulties—the dimensions depended on whether one used the ESU or EMU systems.[47] This anomaly was resolved in 1901 when Giovanni Giorgi published a paper in which he advocated using a fourth base unit alongside the existing three base units. The fourth unit could be chosen to be electric current, voltage, or electrical resistance.[56] Electric current with named unit 'ampere' was chosen as the base unit, and the other electrical quantities derived from it according to the laws of physics. This became the foundation of the MKS system of units.
In the late 19th and early 20th centuries, a number of non-coherent units of measure based on the gram/kilogram, centimetre/metre, and second, such as the Pferdestärke (metric horsepower) for power,[57][Note 11] the darcy for permeability[58] and "millimetres of mercury" for barometric and blood pressure were developed or propagated, some of which incorporated standard gravity in their definitions.[Note 12]
At the end of the Second World War, a number of different systems of measurement were in use throughout the world. Some of these systems were metric system variations; others were based on customary systems of measure, like the U.S customary system and Imperial system of the UK and British Empire.
The Practical system of units[edit]
This section is missing information about changeover centigrade→Kelvin and candlepower→candela. (December 2017)
|
In 1948, the 9th CGPM commissioned a study to assess the measurement needs of the scientific, technical, and educational communities and "to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention".[59] This working document was Practical system of units of measurement. Based on this study, the 10th CGPM in 1954 defined an international system derived from six base units including units of temperature and optical radiation in addition to those for the MKS system mass, length, and time units and Giorgi's current unit. Six base units were recommended: the metre, kilogram, second, ampere, degree Kelvin, and candela.
The 9th CGPM also approved the first formal recommendation for the writing of symbols in the metric system when the basis of the rules as they are now known was laid down.[60]These rules were subsequently extended and now cover unit symbols and names, prefix symbols and names, how quantity symbols should be written and used, and how the values of quantities should be expressed.[2]:104,130
Birth of the SI[edit]
In 1960, the 11th CGPM synthesised the results of the 12-year study into a set of 16 resolutions. The system was named the International System of Units, abbreviated SI from the French name, Le Système International d'Unités.[2]:110[61]
Historical definitions[edit]
When Maxwell first introduced the concept of a coherent system, he identified three quantities that could be used as base units: mass, length, and time. Giorgi later identified the need for an electrical base unit, for which the unit of electric current was chosen for SI. Another three base units (for temperature, amount of substance, and luminous intensity) were added later.
The early metric systems defined a unit of weight as a base unit, while the SI defines an analogous unit of mass. In everyday use, these are mostly interchangeable, but in scientific contexts the difference matters. Mass, strictly the inertial mass, represents a quantity of matter. It relates the acceleration of a body to the applied force via Newton's law, F = m × a: force equals mass times acceleration. A force of 1 N (newton) applied to a mass of 1 kg will accelerate it at 1 m/s2. This is true whether the object is floating in space or in a gravity field e.g. at the Earth's surface. Weight is the force exerted on a body by a gravitational field, and hence its weight depends on the strength of the gravitational field. Weight of a 1 kg mass at the Earth's surface is m × g; mass times the acceleration due to gravity, which is 9.81 newtons at the Earth's surface and is about 3.5 newtons at the surface of Mars. Since the acceleration due to gravity is local and varies by location and altitude on the Earth, weight is unsuitable for precision measurements of a property of a body, and this makes a unit of weight unsuitable as a base unit.
| Unit name | Definition[n 1] |
|---|---|
| second |
|
| metre |
|
| kilogram |
|
| ampere |
|
| kelvin |
|
| mole |
|
| candela |
|
The Prior definitions of the various base units in the above table were made by the following authorities:
All other definitions result from resolutions by either CGPM or the CIPM and are catalogued in the SI Brochure.
| |
The SI base units are seven units of measure defined by the International System of Units as the basic set from which all other SI units can be derived. The units and their physical quantities are the second for time, the metre for measurement of length, the kilogram for mass, the ampere for electric current, the kelvin for temperature, the mole for amount of substance, and the candela for luminous intensity.
The SI base units form a set of mutually independent dimensions as required by dimensional analysis commonly employed in science and technology.
The names and symbols of SI base units are written in lowercase, except the symbols of those named after a person, which are written with an initial capital letter. For example, the metre (US English: meter) has the symbol m, but the kelvin has symbol K, because it is named after Lord Kelvin and the ampere with symbol A is named after André-Marie Ampère.
A number of other units, such as the litre (US English: liter), astronomical unit and electronvolt, are not formally part of the SI, but are accepted for use with SI.
Definitions[edit]
On 20 May 2019, as the final act of the 2019 redefinition of the SI base units, the BIPM officially introduced the following new definitions, replacing the preceding definitions of the SI base units.
| Name | Symbol | Measure | Post-2019 formal definition[1] | Historical origin / justification | Dimension symbol |
|---|---|---|---|---|---|
| second | s | time | "The second, symbol s, is the SI unit of time. It is defined by taking the fixed numerical value of the caesium frequency ∆νCs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9192631770 when expressed in the unit Hz, which is equal to s−1."[1] | The day is divided in 24 hours, each hour divided in 60 minutes, each minute divided in 60 seconds. A second is 1 / (24 × 60 × 60) of the day. Historically this day was defined as the mean solar day; i.e., the average time between two successive occurrences of local apparent solar noon. | T |
| metre | m | length | "The metre, symbol m, is the SI unit of length. It is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299792458 when expressed in the unit m s−1, where the second is defined in terms of ∆νCs."[1] | 1 / 10000000 of the distance from the Earth's equator to the North Pole measured on the median arc through Paris. | L |
| kilogram | kg | mass | "The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J s, which is equal to kg m2 s−1, where the metre and the second are defined in terms of c and ∆νCs."[1] | The mass of one litre of water at the temperature of melting ice. A litre is one thousandth of a cubic metre. | M |
| ampere | A | electric current | "The ampere, symbol A, is the SI unit of electric current. It is defined by taking the fixed numerical value of the elementary charge e to be 1.602176634×10−19 when expressed in the unit C, which is equal to A s, where the second is defined in terms of ∆νCs."[1] | The original "International Ampere" was defined electrochemically as the current required to deposit 1.118 milligrams of silver per second from a solution of silver nitrate. Compared to the SI ampere, the difference is 0.015%. However, the most recent pre-2019 definition was: "The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one metre apart in vacuum, would produce between these conductors a force equal to 2×10−7newtons per metre of length." This had the effect of defining the vacuum permeability to be | I |
| kelvin | K | thermodynamic temperature | "The kelvin, symbol K, is the SI unit of thermodynamic temperature. It is defined by taking the fixed numerical value of the Boltzmann constant k to be 1.380649×10−23 when expressed in the unit J K−1, which is equal to kg m2 s−2 K−1, where the kilogram, metre and second are defined in terms of h, c and ∆νCs."[1] | The Celsius scale: the Kelvin scale uses the degree Celsius for its unit increment, but is a thermodynamic scale (0 K is absolute zero). | Θ |
| mole | mol | amount of substance | "The mole, symbol mol, is the SI unit of amount of substance. One mole contains exactly 6.022 140 76 × 1023 elementary entities. This number is the fixed numerical value of the Avogadro constant, NA, when expressed in the unit mol−1 and is called the Avogadro number. The amount of substance, symbol n, of a system is a measure of the number of specified elementary entities. An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles."[1] | Atomic weight or molecular weight divided by the molar mass constant, 1 g/mol. | N |
| candela | cd | luminous intensity | "The candela, symbol cd, is the SI unit of luminous intensity in a given direction. It is defined by taking the fixed numerical value of the luminous efficacy of monochromatic radiation of frequency 540×1012 Hz, Kcd, to be 683 when expressed in the unit lm W−1, which is equal to cd sr W−1, or cd sr kg−1 m−2 s3, where the kilogram, metre and second are defined in terms of h, c and ∆νCs."[1] | The candlepower, which is based on the light emitted from a burning candle of standard properties. | J |
| Name | Symbol | Measure | Post-2019 formal definition[1] | Historical origin / justification | Dimension symbol |
2019 redefinition of SI base units[edit]
New definitions of the base units were approved on 16 November 2018, and took effect 20 May 2019. The definitions of the base units have been modified several times since the Metre Convention in 1875, and new additions of base units have occurred. Since the redefinition of the metre in 1960, the kilogram had been the only base unit still defined directly in terms of a physical artefact, rather than a property of nature. This led to a number of the other SI base units being defined indirectly in terms of the mass of the same artefact; the mole, the ampere, and the candela were linked through their definitions to the mass of the International Prototype of the Kilogram, a roughly golfball-sized platinum–iridium cylinder stored in a vault near Paris.
It has long been an objective in metrology to define the kilogram in terms of a fundamental constant, in the same way that the metre is now defined in terms of the speed of light. The 21st General Conference on Weights and Measures (CGPM, 1999) placed these efforts on an official footing, and recommended "that national laboratories continue their efforts to refine experiments that link the unit of mass to fundamental or atomic constants with a view to a future redefinition of the kilogram". Two possibilities attracted particular attention: the Planck constant and the Avogadro constant.
In 2005, the International Committee for Weights and Measures (CIPM) approved preparation of new definitions for the kilogram, the ampere, and the kelvin and it noted the possibility of a new definition of the mole based on the Avogadro constant.[2] The 23rd CGPM (2007) decided to postpone any formal change until the next General Conference in 2011.[3][needs update]
In a note to the CIPM in October 2009,[4] Ian Mills, the President of the CIPM Consultative Committee – Units (CCU) catalogued the uncertainties of the fundamental constants of physics according to the current definitions and their values under the proposed new definition. He urged the CIPM to accept the proposed changes in the definition of the kilogram, ampere, kelvin, and mole so that they are referenced to the values of the fundamental constants, namely the Planck constant (h), the electron charge (e), the Boltzmann constant (k), and the Avogadro constant (NA).[5] This approach was approved in 2018, only after measurements of these constants were achieved with sufficient accuracy.
The SI rests on a foundation of seven (7) defining constants: the cesium hyperfine splitting frequency, the speed of light in vacuum, the Planck constant, the elementary charge (i.e. the charge on a proton), the Boltzmann constant, the Avogadro constant, and the luminous efficacy of a specified monochromatic source. Definitions of all seven (7) SI base units are expressed using an explicit-constant formulation and experimentally realized using a specific mises en pratique (practical technique).
The seven SI base units, which are comprised of:
- Length - meter (m)
- Time - second (s)
- Amount of substance - mole (mole)
- Electric current - ampere (A)
- Temperature - kelvin (K)
- Luminous intensity - candela (cd)
- Mass - kilogram (kg)
The International System of Units (SI), commonly known as the metric system, is the international standard for measurement. The International Treaty of the Meter was signed in Paris on May 20, 1875 by seventeen countries, including the United States and is now celebrated around the globe as World Metrology Day. NIST provides official U.S. representation in the various international bodies established by the Meter Convention: CGPM - General Conference on Weights and Measures; CIPM - International Committee for Weights and Measures; and BIPM - The International Bureau of Weights and Measures.
The SI is made up of 7 base units that define the 22 derived units with special names and symbols. The SI plays an essential role in international commerce and is commonly used in scientific and technological research and development. Learn more about the SI in NIST SP 330 and SP 811.
Redefining the SI
In November 2018, the world’s measurement experts voted and unanimously approved a revision of the SI that establishes a measurement system entirely based on physical constants of nature. The changes became effective on World Metrology Day, May 20, 2019.
Learn more about the Road to the Revised SI. Learn more about the SI Redefinition.
NIST Metric Trivia Quiz
How much do you know about the metric system (SI)? Try the NIST Metric Trivia Quiz online or use the Alexa skill to test your knowledge and be on your way to thinking metric!
SI base unitsThe SI is founded on seven SI base units for seven base quantities assumed to be mutually independent, as given in Table 1.
SI derived units Other quantities, called derived quantities, are defined in terms of the seven base quantities via a system of quantity equations. The SI derived units for these derived quantities are obtained from these equations and the seven SI base units. Examples of such SI derived units are given in Table 2, where it should be noted that the symbol 1 for quantities of dimension 1 such as mass fraction is generally omitted.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For ease of understanding and convenience, 22 SI derived units have been given special names and symbols, as shown in Table 3.
SI Units, Symbols & AbbreviationsThe chart below gives the standard abbreviations and symbols for the major quantities measured using SI units - the International System of Units.
SI, International System of Units Includes:
SI base units SI units & symbols SI / metric prefixes Unit definitions SI (metric) / Imperial conversion
There are many abbreviations used to denote different measurements and quantities. The chances are that any scientific measurement or quantity will be measured using SI Units - the International System of Units.
There are many standard abbreviations and symbols used with these quantities. The SI, System International units, symbols and abbreviations are well defined and documented and provide the basis for the way most scientific quantities (as well as many others) are quoted and measured.
The SI unit symbols for quantities such as current, voltage and the like, are very common, and within electrical or electronic circles.
However when an unfamiliar unit symbol is first used within a paper or other document, it should be followed by its name in parentheses. In this way readers who may not be familiar with the particular unit symbol may be able to understand it.
SI unit symbol & abbreviation usage
When writing SI unit symbols, they are written in lower case except for cases where the unit is derived from a proper name, or in the very few cases where the abbreviation is not formed from a letter.
The definition for methods of writing SI symbols states that the symbols for the units should not be followed by a period / full stop. In other words a current of ten amperes is written 10A, and not 10A., although punctuation for sentences still applies.
When a compound unit SI unit symbols is made by multiplying two or more other units, its overall symbol should consist of the symbols for the separate units joined by dots which are raised, i.e. ⋅ . However the raised dot, may be omitted in the case of familiar compound unit symbols.
For example both V ⋅ s and V s are acceptable.
Table of the SI units, symbols, & abbreviations
The table above gives some of the most commonly used SI symbols, units and abbreviations which are seen in scientific and engineering applications.
The 7 Fundamental SI Units
International System of Units
International System of Units (SI), French Système Internationale d’Unités, international decimal system of weights and measures derived from and extending the metric system of units. Adopted by the 11th General Conference on Weights and Measures in 1960, it is abbreviated SI in all languages.
Rapid advances in science and technology in the 19th and 20th centuries fostered the development of several overlapping systems of units of measurements as scientists improvised to meet the practical needs of their disciplines. The early international system devised to rectify this situation was called the metre-kilogram-second (MKS) system. The General Conference on Weights and Measures (CGPM) added three new units (among others) in 1948: a unit of force (the newton), defined as that force which gives to a mass of one kilogram an acceleration of one metre per second per second; a unit of energy (the joule), defined as the work done when the point of application of a newton is displaced one metre in the direction of the force; and a unit of power (the watt), which is the power that in one second gives rise to energy of one joule. All three units are named for eminent scientists.
The 1960 International System builds on the MKS system. Its seven basic units, from which other units are derived, were defined as follows: for length, the metre, defined as the distance traveled by light in a vacuum in 1/299,792,458 second; for mass, the kilogram, which equaled 1,000 grams as defined by the international prototype kilogram of platinum-iridium in the keeping of the International Bureau of Weights and Measures in Sèvres, France; for time, the second, the duration of 9,192,631,770 periods of radiation associated with a specified transition of the cesium-133 atom; for electric current, the ampere, which was the current that, if maintained in two wires placed one metre apart in a vacuum, would produce a force of 2 × 10−7 newton per metre of length; for luminous intensity, the candela, defined as the intensity in a given direction of a source emitting radiation of frequency 540 × 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian; for amount of substance, the mole, defined as containing as many elementary entities of a substance as there are atoms in 0.012 kg of carbon-12; and for thermodynamic temperature, the kelvin.
The CGPM in 2018 agreed to a proposal that from May 20, 2019, the kilogram, the ampere, the mole, and the kelvin would be redefined in terms of fundamental physical constants. For the kilogram, the constant chosen was Planck’s constant, which would be defined to be equal to 6.62607015 × 10−34 joule second. One joule is equal to one kilogram times metre squared per second squared. Since the second and the metre were already defined, the kilogram would then be determined by accurate measurements of Planck’s constant. The ampere would be redefined such that the elementary charge would be equal to 1.602176634 × 10−19 coulomb. The kelvin would be redefined such that the Boltzmann constant would be equal to 1.380649 × 10−23 joule per kelvin, and the mole would be redefined such that the Avogadro constant would be equal to 6.02214076 × 1023 per mole.
Widely used units in the SI system
A list of the widely used units in the SI system is provided in the table.
Metric conversions
A list of metric conversions is provided in the table.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||